- (a)
- Definición de la clase Rectángulo:
class Rectangle inherits from Point { attributes: int _width, // Base del rectángulo _height // Altura del rectángulo methods: setWidth(int newWidth) getWidth() setHeight(int newHeight) getHeight() }En este ejemplo, definimos un rectángulo por su esquina superior izquierda (las coordenadas tal como se heredaron de Point) y sus dimensiones. Alternativamente, lo podríamos haber definido por su esquina superior izquierda y su esquina inferior derecha.
Añadimos métodos de acceso para la base y la altura del rectángulo.
- (b)
- Objetos en 3a. dimensión.
Una esfera se define por un centro en un espacio en 3a. dimensión, y por un radio. El centro es un punto en un espacio en 3a. dimensión, así, podemos definir la clase
Sphere (esfera) como:
class Sphere inherits from 3D-Point { attributes: int _radius; methods: setRadius(int newRadius) getRadius() }Esto es similar a la clase círculo para un espacio en 2a. dimensión. Ahora3D-Point es solamente un Point con una dimensión adicional:
class 3D-Point inherits from Point { attributes: int _z; methods: setZ(int newZ); getZ(); }Consecuentemente, 3D-Point y Point tienen una relación es-un(a).
- (c)
- Funcionalidad de move().
move() como se definió en la sección le permite a los objetos de 3a. dimensión moverse a lo largo del eje-X, es decir, en una sola dimensión. Hace esto, al modificar solamente la parte de 2a. dimensión de los objetos de 3a. dimensión. Esta parte de 2a. dimensión está definida por la clase Point heredada directamente o indirectamente por los objetos de 3a. dimensión.
- (d)
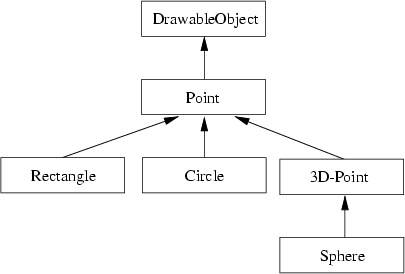
- Gráfica de herencia (ver la Figura A.1).
- (e)
- Gráfica de herencia alternativa. En este ejemplo, la clase Sphere hereda de Circle y simplemente añade una tercera coordenada. Esto tiene la ventaja de que una esfera puede ser manejada como un círculo (por ejemplo, su radio puede ser fácilmente modificado por métodos/funciones que manejan círculos). Tiene la desventaja de que "distribuye" el manejador (el centro en el espacio de 3a. dimensión) sobre la jerarquía de herencia : va desde Point pasando sobre Circle a Sphere. De ahí que este manejador no esté accesible como un todo.
Sin embargo, estas propiedades se identifican en forma única siguiendo la trayectoria hacia arriba desde D hasta A. Así, D puede cambiar las propiedades de A heredadas por B al seguir la trayectoria de herencia a través de B. En forma similar, D puede cambiar las propiedades de A heredadas por C al seguir la trayectoria de herencia a través de C. Consecuentemente, este conflicto de nomenclatura no necesariamente conlleva a error, mientras las trayectorias estén designadas.